Comportement sous déformation des mousses
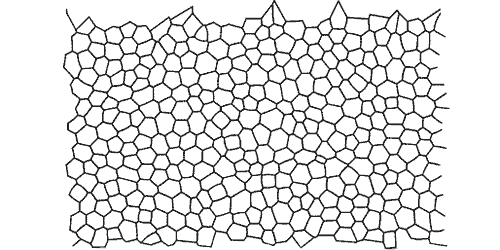
La structure au repos d'une mousse correspond à celle qui offre la plus petite surface de film de savon, compte tenu de l'organisation particulière des bulles entre elles et de leur volume. Cette propriété exceptionnelle permet de calculer précisément, à l'aide d'un ordinateur, la forme exacte d'un ensemble de bulles dont on connaît les relations de voisinage.
Si l'on déforme légèrement une mousse, l'ensemble de la structure s'adapte à la déformation en modifiant la forme et la superficie des différents films liquides. Il arrive alors que certains films voient leur taille devenir si petite que la structure se déstabilise, conduisant alors à des réarrangements de bulles, c'est à dire à une évolution des relations de voisinage. La structure de la mousse après le réarrangement peut alors être recalculée en minimisant la surface totale de film compte tenu des nouvelles relations de voisinage.
Ces différents éléments conduisent à une modélisation numérique simple du comportement des mousses sous déformation lente. Considérons une mousse, calculée numériquement, confinée à deux dimensions (cf. article). Plaçons cette mousse entre deux parois rigides (bords supérieur et inférieur), et déplaçons horizontalement une des parois par de petits incréments successifs (ce type de déformation se nomme cisaillement). Pour chacun de ces incréments, calculons la structure de surface minimale. Si un film de très faible taille apparaît, modifions l'organisation des bulles selon le schéma d'un T1, décrit dans le corps de l'article, puis recalculons la structure de surface minimale. Si plus aucun réarrangement ne doit être réalisé, continuons alors à augmenter, toujours par incrément, la déformation, jusqu'à ce que de nouveaux réarrangements soient nécessaires, et ainsi de suite.
Les animations suivantes ont été obtenues en utilisant un tel algorithme. Afin de palier à la faible taille des systèmes qu'il est possible d'étudier numériquement en un temps raisonnable, il est commun d'utiliser ce que l'on appelle des conditions limites périodiques, à savoir que l'extrémité gauche de la mousse est "numériquement" reliée l'extrémité droite. Cette artifice permet de créer fictivement un système périodique de taille infinie. Ainsi, dans notre exemple, une bulle qui, suite au déplacement de la paroi, disparaît par la droite, réapparaît à gauche, et réciproquement. Deux images successives de ces animations sont séparées soit par un incrément de déplacement du mur, soit par un réarrangement de bulle. Les bulles qui se réarrangent sont représentées en couleur sur l'image suivant le réarrangement ; il est ainsi aisé de visualiser la position des réarrangements.
Sur les deux exemples suivants, nous soumettons la mousse à un cisaillement alterné ; pour cela, nous déplaçons alternativement la paroi sur une distance donnée vers la gauche puis vers la droite. Pour une faible amplitude de déformation maximale, après quelques réarrangements transitoires, plus aucun réarrangement n'apparaît. Il s'agit du régime élastique aux petites déformations. Pour de plus grandes amplitudes, un tel régime n'existe pas : la mousse cède systématiquement en générant des avalanches de réarrangements.
amplitude de déformation : +/- 30%
amplitude de déformation : +/- 100%


