A general
body is analyzed to demonstrate the application of Newton's
laws to angular motion in 3-D
Newton's second law is applied to particle i, giving:
From this moments are taken about point P (note that P is not necessarily stationary):
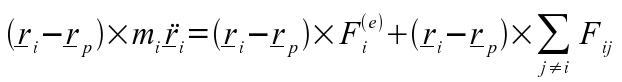
The result of this is summed over all particles in the body giving (A):
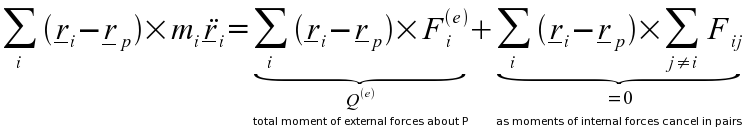
The total moment of momentum about P is given by:
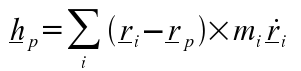
When this is differentiated with respect to time the following is obtained:
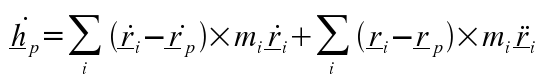
If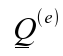
from equation (A) is substituted
into the above equation it becomes:
(B)
The linear momentum, P of a body is given by:
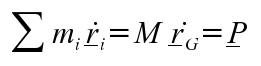
This can then be substituted into equation (B) to give a key result:
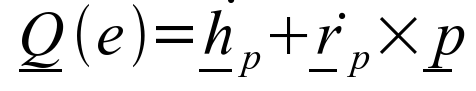
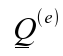= Total moment of
the
external forces
=
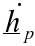Rate of
change of total moment of momentum
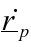= Velocity of point P
=
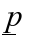Total linear momentum
This is a key equation when dealing with angular motion in 3-D
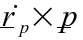Accounts for the fact that the point P may be moving. If P is at the
center of mass,
G or a fixed point
the equation simplifies to:
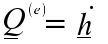
Contrary to laithwaite's claims angular motion in 3-D does not have some force all of its own, it can be described using the formula derived from Newton's second law. This equation is used in the analysis of the repeated Laithwaite videos and it can be seen that it holds for all cases, therefore contrary to Laithwaite's claims Newton's laws of motion apply to objects other than just those that travel in straight lines where there is no rate of change of acceleration, they must first be manipulated so they apply to angular motion of bodies in 3-D.
Newton's second law is applied to particle i, giving:
From this moments are taken about point P (note that P is not necessarily stationary):
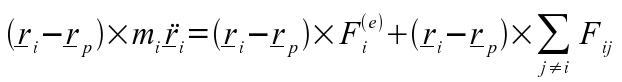
The result of this is summed over all particles in the body giving (A):
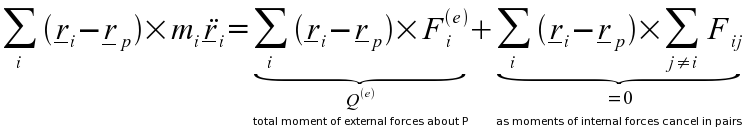
The total moment of momentum about P is given by:
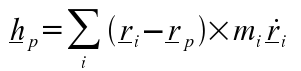
When this is differentiated with respect to time the following is obtained:
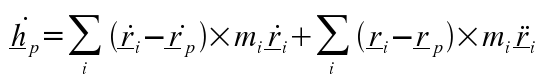
If
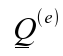from equation (A) is substituted
into the above equation it becomes:
(B)The linear momentum, P of a body is given by:
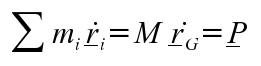
This can then be substituted into equation (B) to give a key result:
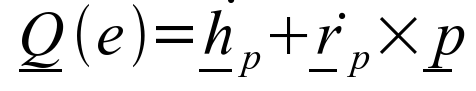
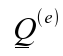= Total moment of
the
external forces =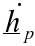
Rate of
change of total moment of momentum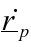
= Velocity of point P
=
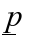Total linear momentum This is a key equation when dealing with angular motion in 3-D
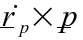Accounts for the fact that the point P may be moving. If P is at the
center of mass,
G or a fixed point
the equation simplifies to: 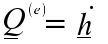Contrary to laithwaite's claims angular motion in 3-D does not have some force all of its own, it can be described using the formula derived from Newton's second law. This equation is used in the analysis of the repeated Laithwaite videos and it can be seen that it holds for all cases, therefore contrary to Laithwaite's claims Newton's laws of motion apply to objects other than just those that travel in straight lines where there is no rate of change of acceleration, they must first be manipulated so they apply to angular motion of bodies in 3-D.