Precession of a gyroscope on a long arm
In this demonstration Laithwaite uses a gyroscope on a long arm that can rotate about a vertical axis. This arm is supported on a pivot point that can be clamped, when unclamped the arm is free to move up and down.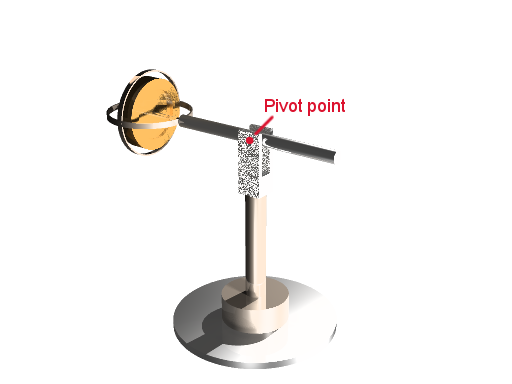
The experiment was repeated using a stand similar to that of Laithwaite's.
(1) Pivot point unclamped
(2) Pivot point clamped

Stand with pivot point clamped
Explanation
of what is happening
The general motion assuming frictionless conditions is explained below.
(1) Pivot point unclamped
The following free body diagrams show the forces acting in this case.
 The
gyroscope is
precessing with speed,
The
gyroscope is
precessing with speed, 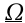 and so the d'Alembert force,
and so the d'Alembert force, (where R is the radius of the circle of precession, i.e. the distance
between the pivot point and the center of mass of the rotor) is also
marked
on the
diagram.
(where R is the radius of the circle of precession, i.e. the distance
between the pivot point and the center of mass of the rotor) is also
marked
on the
diagram.
It can be seen that in the free body diagram of the base all the forces are coincident and so moment equilibrium and force equilibrium are satisfied. However, in the free body diagram of the arm it can be seen that force equilibrium is observed, but moment equilibrium is not.
The arm is able to pivot freely about the pivot point, therefore, the pivot point cannot transmit a moment and can be modeled as a pin joint. From the free body diagram of the arm it can be seen that the offset of the weight of the rotor and reaction results in an external couple. The magnitude of this couple is given by the distance between the rotors center of mass and the pivot point times mg.Since moment equilibrium does not exist there is an overall couple, Q (recall
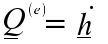 if the point P is stationary - as is the pivot point) and so precession can occur. The
gyroscope is held up because the moment of its weight about the support
is balanced by the change in direction of h.
if the point P is stationary - as is the pivot point) and so precession can occur. The
gyroscope is held up because the moment of its weight about the support
is balanced by the change in direction of h.If the precession of the gyroscope is slow
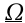 is therefore small and the d'Alembert force may be treated as
negligible and ignored. In this case the free body diagrams
are as
follows.
is therefore small and the d'Alembert force may be treated as
negligible and ignored. In this case the free body diagrams
are as
follows. 
It can be seen that there is still a net overall couple acting. This is again due to the fact that the pivot point cannot transmit a moment. Therefore, as before due to the fact that Q is non zero precession occurs.
If the precession is fast, then the d'Alembert force is large. The following is a free body diagram for when
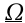 is large.
is large.

In this case it can be seen that the d'Alembert force is large. This has resulted in the reaction force at the base being outside the base. Therefore, in this case the stand would topple as the reaction force must act within the base.
It can be seen that for fast precession the base must be sufficiently large to ensure that the reaction force acts within it and toppling does not occur
(2) Pivot point clamped
When the pivot point is clamped precession does not occur.
The following is a diagram of the forces acting when the pivot point is clamped.

It can be seen that force and moment equilibrium are observed. The position of the reaction force is given by p and q which are determined by the formula shown on the diagram.
A free body diagram of the arm and clamp can be drawn as follows

When the arm is clamped a moment can be transmitted. This moment balances with the moment caused by the offset of the weight and reaction forces of the rotor. It can be seen from the above diagram that the overall moment is zero, moment equilibrium exists, meaning that Q=0. Since there is no net overall couple there can be no precession. This is observed in the video.
If the base is too small, then the reaction force acts outside the base, and so the stand topples over. The following diagram shows the forces acting when this is the case.

When one attempts to push round the clamped gyro it falls over
If the gyroscope is clamped precession does not occur. When one attempts to push the arm round to the same precession rate as before (in the case where the stand is large enough that it does not topple initially) the stand topples. This is because by pushing the arm one changes the direction of spin axis and so the direction of h, the moment of momentum vector. This means that
 becomes non zero.
becomes non zero.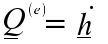 at a
fixed point (pivot point) and so a couple is introduced
by pushing the arm.
at a
fixed point (pivot point) and so a couple is introduced
by pushing the arm. This couple acts about the base of the stand causing it to topple. It can be observed that when the arm is clamped and the gyroscope is not spinning when one pushes the arm it still falls over. This is because the toppling is caused by applying a sudden impulse to the arm.