Euler's Equations
 The
reference frame i, j and k is
aligned with the principle axis of the body. The axes are body fixed
and so the i, j, k
reference frame
moves with the body.
The
reference frame i, j and k is
aligned with the principle axis of the body. The axes are body fixed
and so the i, j, k
reference frame
moves with the body.The moment of momentum can be defined as

Reference frame
Using a body fixed reference frame, aligned with the principle axis ensures that the elements of
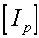 (inertia matrix) don't
change
(inertia matrix) don't
changeThe I, J, K axes are space fixed
In the body fixed reference frame (i, j, k) the instantaneous angular velocity,
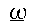 can be defined as
can be defined as 
Using the inertia matrix and the fact that
 along with
the above definition for
along with
the above definition for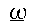 gives the following expression for
moment of momentum.
gives the following expression for
moment of momentum.
 (A)
(A)Since i, j and k move with the body this equation always holds.
Differentiating the above expression gives
 (B)
(B)
From the application of Newton's Laws of Motion to circular motion we know the following is true
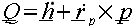
If P is stationary or at the center of mass, G then
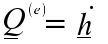 (C)
(C) can be expressed
as
can be expressed
as 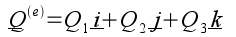
From (A)

From this
 (D)
(D)Using the expanded definitions of
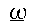 and hp the following
expression for
and hp the following
expression for  is obtained
is obtained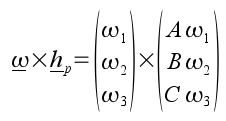
Where x represents the vector cross product. Expanding the above equation gives
 (E)
(E) Substituting (E), (C) and (D) into equation (B) gives:
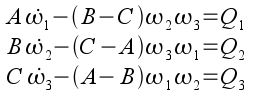
These are EULER'S EQUATIONS in a body fixed axis frame. They determine the angular motion of a body subject to an external couple Q about a point P which MUST either be a FIXED POINT or at G.
Axisymmetric bodies: The Gyroscope equations
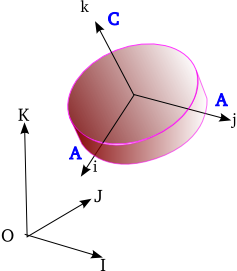
For an axisymmetric body (e.g.: rotor of a gyroscope) the moment of inertia is the same for all i and j within the i-j plane. This is true for all AAC bodies. The k axis is aligned with C and so i, j and k are always aligned with principle axis.
The reference frame moves with angular velocity
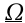 where
where 
The body itself has angular velocity
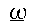 where
where 
In addition to being axisymmetric about the k axis the a gyroscope spins within the reference frame about the k axis. Therefore
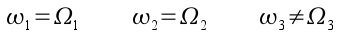
For AAC bodies (such as gyroscopes) EULER'S EQUATIONS become
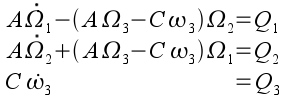
These are the GYROSCOPE EQUATIONS. Euler's angles are used to solve them.